Introdução ao Domínio Colorido em Funções Complexas

Este estudo explora o comportamento visual de funções complexas por meio de domínios coloridos, utilizando a fase e a magnitude para revelar características matemáticas, como polos, zeros e simetrias. A abordagem visual permite uma compreensão intuitiva e aprofundada de conceitos abstratos, facilitando a análise de singularidades e padrões. A seguir, apresentamos alguns exemplos que ilustram essas propriedades.

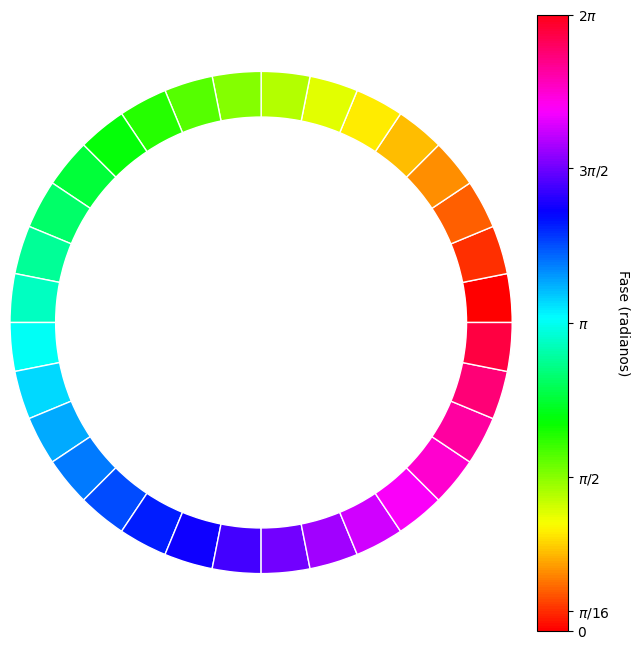
O domínio colorido é uma técnica utilizada para visualizar a fase de funções complexas de maneira intuitiva. Cada ponto z no plano complexo tem sua fase (ângulo) representada por uma cor específica, utilizando a função ψ(z) = z/|z|, que mapeia cada ponto para uma cor baseada no ângulo de z. Neste processo, utilizamos o colormap HSV (Hue, Saturation, Value), que representa o ciclo de cores em um círculo, onde cada cor corresponde a uma fase diferente.

O colormap HSV é ideal para este tipo de visualização, pois o ângulo de fase varia de 0 a 2π, e o esquema de cores HSV mapeia essa variação para cores ao longo de um espectro circular. O uso do HSV permite visualizar claramente as mudanças suaves na fase ao longo do plano complexo.

No exemplo a seguir, mostramos como esse mapeamento de fase é realizado visualmente, usando um anel dividido em setores com diferentes cores, cada uma representando um ângulo de fase. A criação desse anel de cores permite que a fase de uma função complexa seja representada graficamente.

Exemplos de Funções Complexas

• Função f(z) = Re(z²ⁱ)
• Função f(z) = z^2/3+i
• Função f(z) = sin(z⁻²)
• Função f(z) = ½ [senh(z³)] - (1 + i)

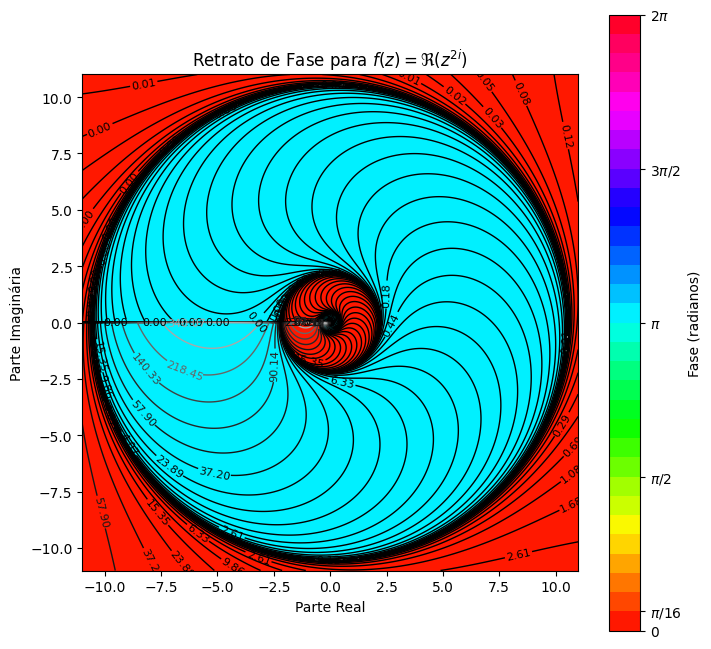
Função f(z) = Re(z2i)

Esta função apresenta um retrato de fase em espiral com cores contrastantes de azul e vermelho. A espiral central representa a interação entre a parte imaginária do expoente e a magnitude do argumento, criando uma composição única onde o valor real da função oscila entre positivo e negativo.

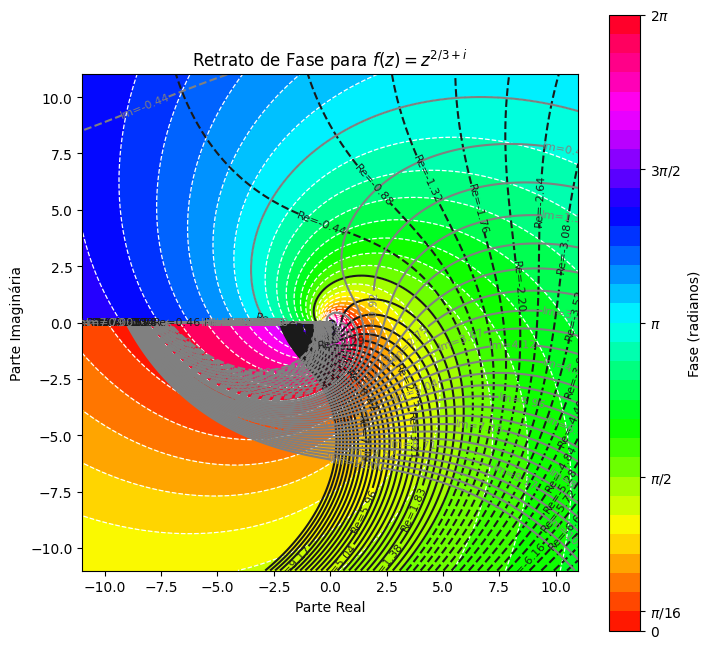
Função f(z) = z2/3+i

Aqui, o comportamento da função é representado com uma estrutura espiral em torno da origem, uma característica comum em funções com expoentes complexos. Este retrato exibe a complexidade da função e a influência de uma base irracional na fase, revelando uma organização de contornos circulares com alternância de cores no gradiente.

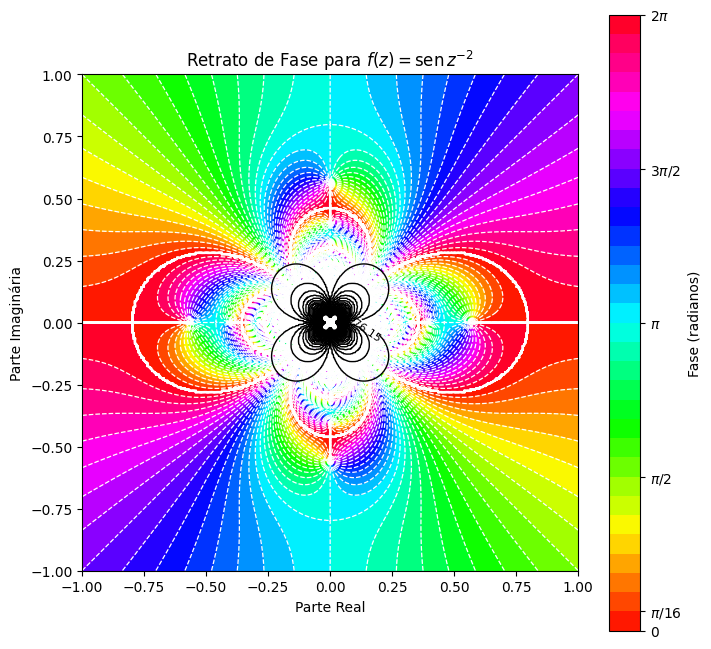
Função f(z) = sin(z⁻²)

Com um polo na origem, essa função mostra um comportamento distinto de rotação ao redor do ponto central. A fase varia rapidamente nas proximidades do polo, enquanto as cores do retrato indicam mudanças de fase em várias direções. A simetria radial é evidente e proporciona uma visão clara da influência do polo na configuração da fase.

Função f(z) = ½ [senh(z³)] - (1 + i)

Esta função gera um retrato de fase com padrões simétricos que se repetem ao longo do plano complexo. A fase é representada por cores, enquanto as linhas de contorno indicam magnitudes constantes da função. Essa configuração destaca regiões de alta simetria e comportamento oscilatório, visualmente marcadas em amarelo e azul.

Acesse o Notebook Completo

Experimente você mesmo: explore as funções complexas no Google Colab e descubra as propriedades de fase e magnitude. Acesse o Notebook Completo.