Curvas simetricas de ordem m

De belas curvas e poliedros com Python

No artigo, "Wheels on Wheels on Wheels-Surprising Symmetry", Frank A. Farris compartilha como, ao criar um exercício para seus alunos, ele desenhou a curva definida pela seguinte equação vetorial:

(x, y) = (cos(t), sin(t)) + 12 (cos(7t), sin(7t)) + 13 (sin(17t), cos(17t))

Farris observa que essa curva possui uma simetria de ordem 6, um fato que, segundo ele, não seria evidente ao olhar para a fórmula. Ele introduz a notação complexa para demonstrar que, de forma mais geral, a curva resultante exibirá uma simetria de ordem m se as três frequências forem congruentes mod m.

Farris oferece outro belo exemplo, cuja equação é dada por:

f(t) = x(t) + iy(t) = e^{-2it} + 12e^{5it} + i4e^{19it}

A partir dessa estrutura, é possível criar várias curvas incríveis, ajustando os valores de m, as frequências e os coeficientes. A beleza dessas curvas vai além da matemática pura, possibilitando sua aplicação em áreas como criptografia, modelagem física e até na arte.

1. Introdução

As curvas com simetria rotacional de ordem m têm aparecido em várias áreas da matemática e podem ser visualizadas de forma interativa. Através do Google Colab, você pode experimentar diferentes parâmetros para criar novas curvas e explorar sua simetria rotacional. No exemplo de Farris, conseguimos construir uma curva simétrica a partir da seguinte fórmula paramétrica:

γ(t) = ∑ r_j exp(i a_j t)

onde r_j são os raios e a_j as velocidades angulares das componentes rotacionais. Essas curvas apresentam uma beleza única e podem ser usadas para estudar diversos fenômenos geométricos.

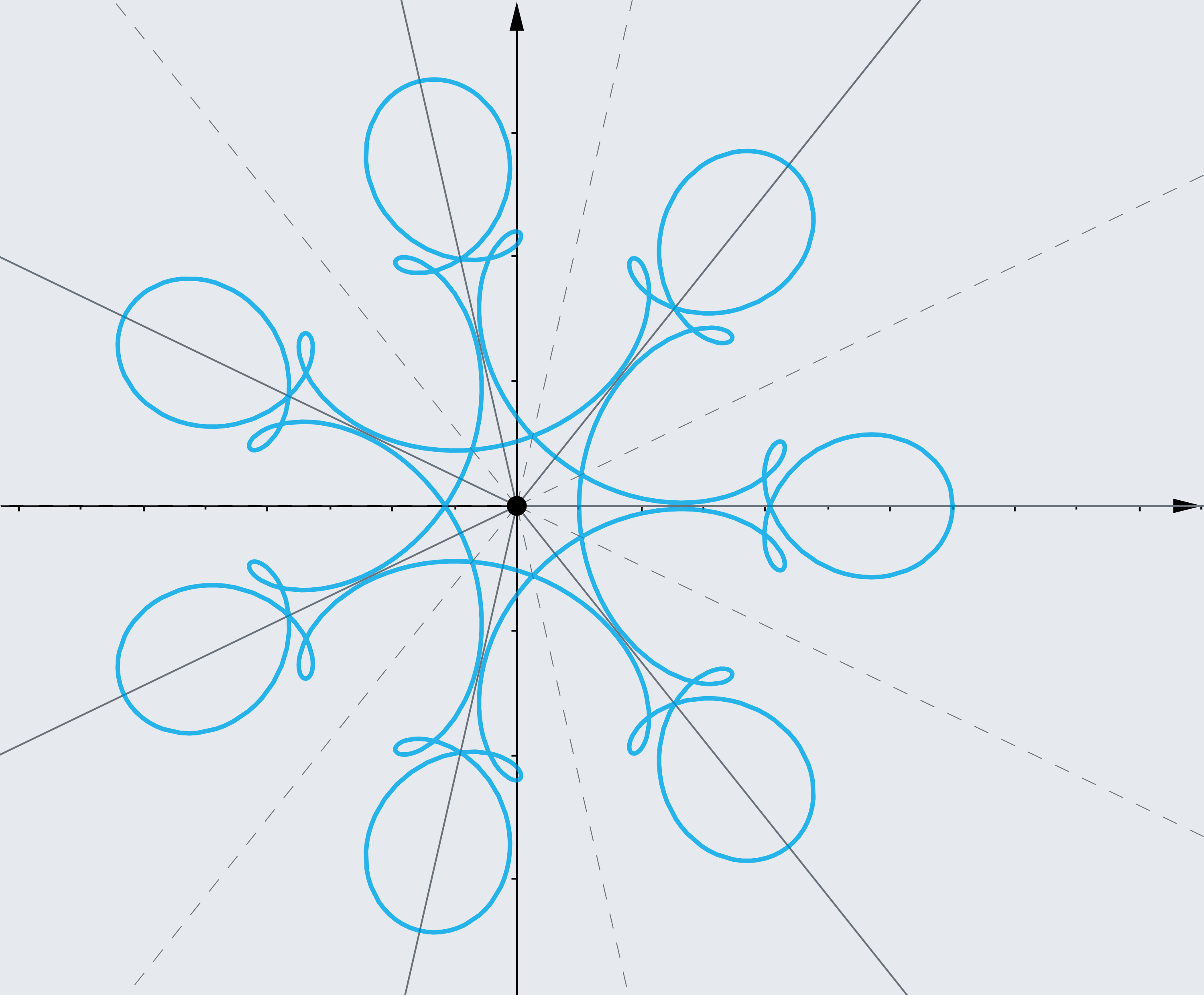
2. Curvas Paralelas e o Vetor Normal

Além de analisar as curvas principais, também é possível estudar as curvas paralelas a partir do vetor normal à curva original. Para isso, utilizamos as seguintes fórmulas para o vetor tangente e o vetor normal:

Vetor Tangente: T(t) = γ'(t)/||γ'(t)||
Vetor Normal: N(t) = Δ_{π/2} T(t)

Essas curvas preservam a simetria rotacional da curva original.

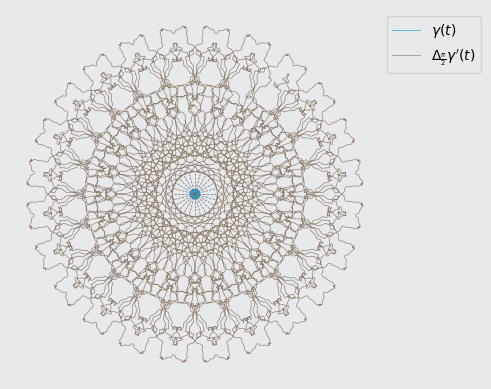
Explorar essas curvas é possível por meio do Google Colab, onde animações e gráficos interativos foram implementados.